A Birthday Integral

2012-10-26 math integral

---

There was a post on math.stackexchange.com where somebody was looking for a non-trivial integral, evaluating to $59$, as a birthday present for his father. In the end, only one answer impressed me. All the rest relied on some transparent encoding of $59$ in the exponents and/or coefficients.

Problem

Show that

$${\int }_0^{\mathrm{\infty }}dx\frac{x^2(x^4-2)}{\cosh (\pi x\mathrm{/}2)}=59.$$

Solution

The polynomial in the numerator is waving a big, red flag at us that we should stick in an exponential factor and repeatedly differentiate it. Let’s instead consider the integral

$$I(a)=\frac{1}{2}\int_{-\infty}^\infty dx,\frac{e^{iax}}{\cosh(\pi x/2)},$$

which is related to the integral of interest through

$$\int_0^\infty dx,\frac{x^2(x^4-2)}{\cosh(\pi x/2)}=\left.\left(\frac{1}{i^6}\frac{d^6}{da^6}-\frac{2}{i^2}\frac{d^2}{da^2}\right)I(a)\right|_{a=0}.\tag{1}$$

We compute $I(a)$ by letting $a>0$ and taking a contour closing in the upper half of the complex plane (where $\mathrm{I}\mathrm{m}x>0$ so that $e^{iax}$ is exponentially damping).

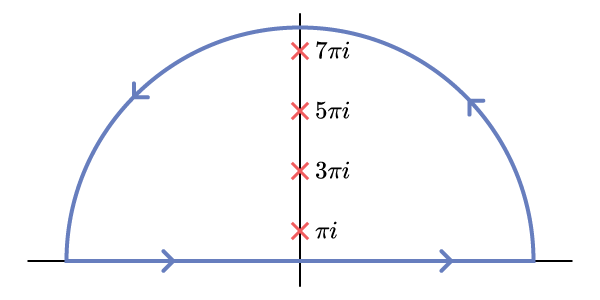
The integrand has poles everywhere that $\cosh (\pi x\mathrm{/}2)=0$, i.e. at odd integer values of $x$ along the imaginary axis. What are the residues there? The poles are all simple, so at $x=(2k+1)i$, with $k\in \mathbb{Z}$, we find

$$\textrm{Res}\left(\frac{e^{iax}}{\cosh(\pi x/2)};;x=(2k+1)i\right)=\left.\frac{e^{iax}}{\frac{d}{dx}\cosh(\pi x/2)}\right|_{x=(2k+1)i}=\frac{2}{\pi i}(-1)^k e^{-a(2k+1)}$$

and the result of the integral, enclosing the poles indexed $k=0,1,2,\dots$, is

$$I(a)=2\pi i\cdot\frac{1}{2}\cdot\frac{2}{\pi i}\sum_{k=0}^\infty (-1)^k e^{-a(2k+1)}=\frac{1}{\cosh a}.$$

The last sum is easily done because it is geometric. So now all that’s left is to differentiate $I(a)$ six times and plug in to compute the original integral. This computation is tedious but straightforward, yielding

$$\frac{d^6 I}{da^6}(a=0)=-61\qquad\qquad\frac{d^2 I}{da^2}(a=0)=-1,$$

so that Eqn. (1) gives

$$\int_0^\infty dx,\frac{x^2(x^4-2)}{\cosh(\pi x/2)}=61-2=59.$$

Going further

Now that we understand the nature of the $59$ coming out of this integral, how can we understand it in a broader sense? We see that it is some sort of a happy accident that this function $I(a)$ encodes the value $61$ which is very close to $59$. What else does it encode? If we look at a Taylor series for small $a$, we have

$$I(a)=\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}a=\frac{1}{0!}+\frac{-1}{2!}{a}^2+\frac{5}{4!}{a}^4+\frac{-61}{6!}{a}^6+\frac{1385}{8!}{a}^8+\dots \mathrm{.}$$

In fact, this $I(a)$ is the exponential generating function for the Euler numbers $E_n$. If we want to engineer this sort of integral to give any other value, we can do it. The coefficients that will come in will be those needed to get the desired value as a linear combination of Euler numbers. It is nice that those numbers will be entirely unrecognizable at first sight, but the original example for $59$ is particularly impressive because there are no big, fishy numbers floating around.

To sum it all up: at the heart of this problem is a nice, simple-looking but not-simple-to-compute integral representation: $${\rm sech},a=\frac{1}{2}\int_{-\infty}^\infty dx,\frac{e^{iax}}{\cosh(\pi x/2)}.$$

From it, we can form linear combinations of its Taylor coefficients by derivatives with respect to $a$. It also helps that this particular function generates an exotic looking sequence.

A similar but less interesting example is furnished by taking the usual integral representation of the $J_0$ Bessel function,

$$J_0(x)=\frac{1}{2\pi}\int_{-\pi}^\pi dt,e^{-ix\sin t}.$$

Then, examining its Taylor series about $x=0$, we can write things like

$$\frac{1}{2\pi}\int_{-\pi}^\pi dt,\left(32\sin^6 t+128\sin^4 t+1\right)=59$$

and

$$\frac{8}{\pi}\int_{-\pi}^\pi dt,\left(16\sin^8 t-7\sin^6 t+4\sin^2 t\right)=59.$$

The coefficients show no obvious link to $59$, but the integrals have elementary anti-derivatives. The principle of how to generate problems like these is clear, though. The hard part is finding a sufficiently nice integral representation (of a function with rational Taylor coefficients).